Home
Movimiento vertical

Movimiento vertical

Cinemática 0

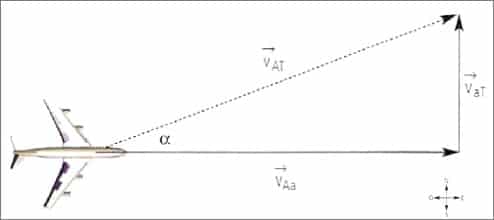
Se habla de movimiento vertical cuando se deja caer un cuerpo, caída libre, o cuando este se lanza verticalmente hacia arriba o hacia abajo.

Tipos de movimiento vertical

Se conocen como movimientos verticales: la caída libre, el lanzamiento vertical hacia arriba y el lanzamiento vertical hacia abajo, los cuales se estudian bajo dos condiciones ideales:

  • Ausencia de roce, es decir, en el vacío.
  • Aceleración de gravedad constante.

Caída libre

Se dice que un cuerpo se encuentra en caída libre cuando se le deja caer al vacío, sin fricción de cualquier otro cuerpo y despreciando el roce con el aire; solo influye en él la aceleración de gravedad.

Al caer, los cuerpos cercanos a la superficie terrestre experimentan una aceleración, llamada aceleración de gravedad (g), debido a la fuerza de atracción gravitatoria. Para alturas no superiores a 10.000 metros el valor de la aceleración de gravedad en la Tierra se puede considerar como 9,8 m/s2 = 10 m/s2
.
La caída libre es un MRUA donde la aceleración siempre es hacia abajo, al igual que el desplazamiento y la velocidad. Como la aceleración de gravedad (g) es considerada constante a bajas alturas y la velocidad inicial (vi) es cero en una caída libre, este movimiento solo depende del tiempo (t) de caída. Las ecuaciones que corresponden a este movimiento son:

    \[ \boxed{ y=y_{i}+v_{i}\; t\; -\frac{1}{2}g\; t^{2}\;\;\;\;\; v_{f}=v_{i}-g\; t \;\;\;\;\;v^{2}_{f}-v^{2}_{i}=-2\; g\; \Delta y } \]

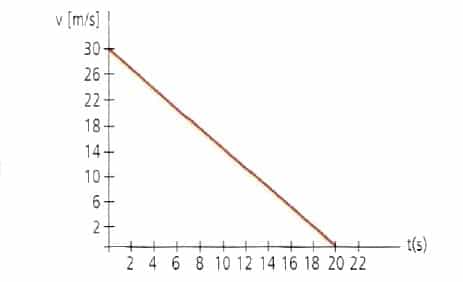
Gráficamente se tiene que:

Movimiento vertical: Caída libre

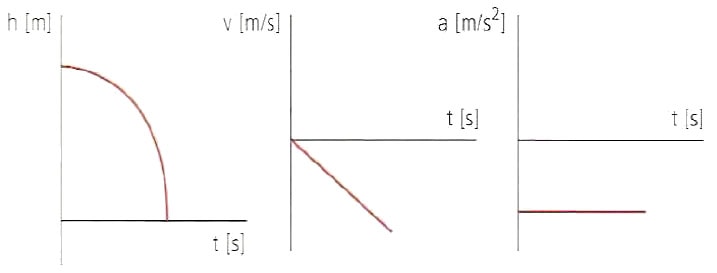
Movimiento vertical: caída libre. La aceleración en caída libre es de 9,8 m en cada segundo, acorde con la aceleración de gravedad.

Lanzamiento vertical hacia arriba

Cuando se realiza un lanzamiento hacia arriba con cierta velocidad inicial, el cuerpo irá disminuyendo su velocidad a 9,8 m/s en cada segundo, acorde con la aceleración de gravedad, hasta llegar a una altura máxima (hmax).

La altura máxima es el punto más alto que alcanza el cuerpo en su trayecto ascendente, donde la velocidad se hará 0, para luego volver a caer en una caída libre. Este tipo de movimiento es uniformemente retardado, pues la aceleración se opone al sentido del movimiento del cuerpo. Las ecuaciones que corresponden a este movimiento son:

    \[ y=y_{i}+v_{i}\;\; t-\frac{1}{2}\;g\;t^{2}\; \; \;\;\;\;\;\;\;\; v_{f}=v_{i}-g\; t \]

    \[ h_{max}=\frac{(v_{i})^{2}}{2g}\; \; \; \; \; \;\; \;\; \;\; \;\; \;\; \; t_{max}=\frac{v_{i}}{g} \]

Movimiento vertical: Lanzamiento vertical hacia arrib

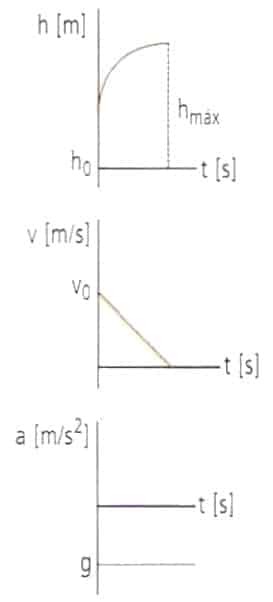
Movimiento vertical: Lanzamiento vertical hacia arriba.

Ejercicio resuelto

1. Un globo aerostático sube verticalmente con una velocidad de 25 [m/s]. Cuando llega a 120 [m] del suelo, deja caer un lastre. ¿Cuánto demora en llegar al suelo?

Datos
\Delta h = -120 [m]
v_{i} = 25 [m/s]
t = ¿?
v=¿?

Para obtener el tiempo, se remplazan los datos en la ecuación de altura. En este caso, para facilitar el cálculo, se aproximará a 10 [m/s2].

    \[ \Delta h=v_{i}\; t-\frac{1}{2}g\; t^{2} \]

    \[ -120 \; m=25\;m/s\;\; t-\frac{10\;m/s^{2}\cdot t^{2}}{2} \]

    \[ -120 \; m=25\;m/s\;\; t-5\;m/s^{2}\ t^{2} \]

Factorizando, 5 pasa dividiendo, por lo que se hace O.

    \begin{align*} 5\; t^{2}-25\;t-120 &=0 \\ 5\;(t^{2}-5\;t-24) &=0 \\ (t+3)(t-8) &=0 \end{align*}

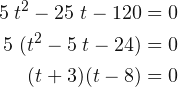
– Si se toma t + 3 = 0, el resultado será -3, siendo un valor negativo, el que no es posible.
– Si se toma t- 8 = 0, el resultado será 8, lo que indica el tiempo que demora en caer el lastre.

Related