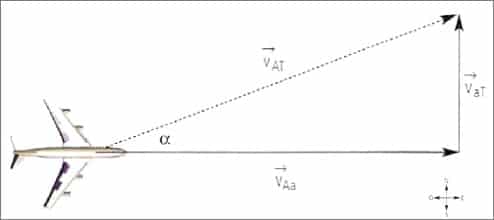
Un movimiento es rectilíneo uniforme si su velocidad permanece constante en todo el intervalo de tiempo. La única trayectoria que acepta esta condición es una trayectoria en línea recta, por lo que el cuerpo recorre distancias iguales en tiempos iguales. Así, la ecuación que describe el movimiento rectilíneo uniforme del cuerpo en esta situación es:
![\[ \boxed{ x=x_{i}+vt} \]](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-90913d24e628984c34915c272afc1db1_l3.png "Rendered by QuickLaTeX.com")
donde:
es la posición del cuerpo en un instante t [s].
es la posición inicial del cuerpo en el tiempo t = 0 [s].
es la velocidad del cuerpo.
Entonces, cuando un cuerpo se mueve de tal modo que su velocidad permanece constante o invariante en el tiempo, se dice que describe un movimiento rectilíneo uniforme, que se abrevia MUR. Esto significa que el cuerpo recorre distancias iguales en intervalos de tiempo iguales (rapidez constante) y sigue una trayectoria recta (sin variar su sentido ni dirección).
Ejemplo:
Gráficas en un movimiento rectilíneo uniforme (MUR)
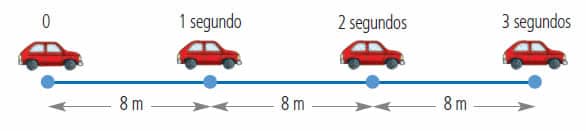
- Gráfico posición-tiempo. En el gráfico posición-tiempo, o también llamado itinerario, el valor de la pendiente corresponde numéricamente a la velocidad, y se obtiene según:
![\[ \boxed{ v=\frac{\Delta x}{\Delta t}} \]](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-45b0c4a0ff684c2214614ec2be4ca255_l3.png "Rendered by QuickLaTeX.com")
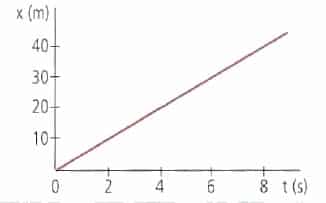
= 0, la posición del móvil, en cada instante, será: x = 5 t.- Gráfico velocidad-tiempo. En un gráfico de velocidad-tiempo, el área bajo la curva representa el camino recorrido del móvil.
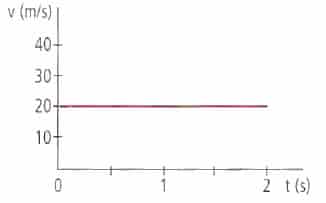
¿Cómo determinamos la distancia recorrida en un MUR?
Si conocemos la velocidad y el tiempo empleado del movimiento rectilíneo uniforme de un cuerpo, podemos determinar la distancia recorrida, que, en este caso, corresponde al desplazamiento. Transformando la relación:
![\[ \boxed{ \vec{v}=\frac{\Delta x}{t}\;\;\;\; \Rightarrow\;\;\;\; x=\vec{v}\cdot \Delta t} \]](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-f46db62b99212e64c3d83cfe8e6f4064_l3.png "Rendered by QuickLaTeX.com")
El mismo valor se obtiene si se calcula el área bajo la curva del gráfico de velocidad-tiempo obtenido.
