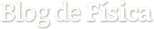En un movimiento armónico simple (MAS), un objeto oscila indefinidamente entre dos posiciones máximas sin perder energía mecánica. En la realidad, debido al roce, estas oscilaciones se amortiguan, a no ser que exista una fuerza externa impulsora. En este caso, la oscilación es forzada.
Siempre que sobre un objeto actúe una fuerza linealmente proporcional al desplazamiento y en dirección opuesta, el objeto experimentará un movimiento armónico simple.
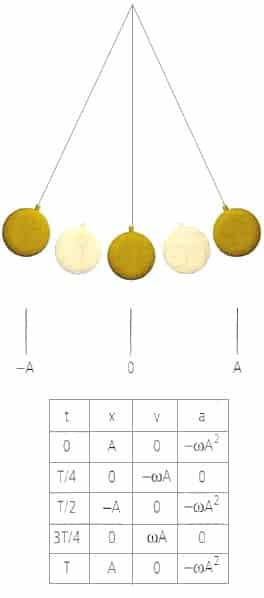
Movimiento armónico simple de un péndulo. La tabla muestra la posición, velocidad y aceleración del movimiento del péndulo obtenidas evaluando las ecuaciones durante un período de tiempo t.
Pueden ser ejemplos de movimiento armónico simple todos aquellos movimientos periódicos como la oscilación de una masa acoplada a un resorte, el movimiento de un péndulo, las ondas electromagnéticas, o el comportamiento de ciertas variables en circuitos de corriente alterna, e incluso, la proyección de movimiento circular uniforme de una partícula sobre su propio diámetro.
Ecuaciones del movimiento armónico simple
La posición de un oscilador armónico simple varía periódicamente con el tiempo según la relación:
![\[ \boxed{ X=A\; cos\; \left ( \omega t+\delta \right )} \]](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-ea74f0691a93d9446f938c09dfca9b9a_l3.png "Rendered by QuickLaTeX.com")
donde:
es la amplitud del movimiento (o máximo desplazamiento).
es la frecuencia angular.
es la constante de fase.
El valor de depende de la posición y la velocidad inicial del oscilador, si este está en fase, 
.
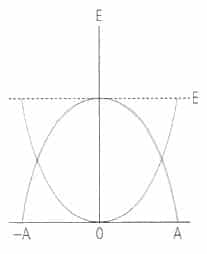
La energía total de un oscilador armónico simple es una constante de movimiento proporcional al cuadrado de la amplitud en la forma: E=1/2 KA2
Como el movimiento es periódico, el tiempo necesario para una oscilación completa es:
![\[ \boxed{ T=\frac{2\pi }{\omega }} \]](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-562e9ea9679c76a909f987d4d91b6ffa_l3.png "Rendered by QuickLaTeX.com")
La frecuencia angular medida en (rad/s) será por lo tanto:
![\[ \boxed{ \omega =\frac{2\pi }{T}} \]](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-08e554d20499a30552e50d1eaa204ac1_l3.png "Rendered by QuickLaTeX.com")
La velocidad de un oscilador armónico simple está dada por:
![\[ \boxed{ v=-\omega A\; sen\left \; ( \omega t+\delta \right )} \]](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-893371e89258c70c592c8d02248af5ec_l3.png "Rendered by QuickLaTeX.com")
La aceleración estará dada por:
![\[ \boxed{ a=-\omega^{2} A\; cos\left \; ( \omega t+\delta \right )} \]](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-5583eb2a39ff1eaadd35aecd2d063f44_l3.png "Rendered by QuickLaTeX.com")
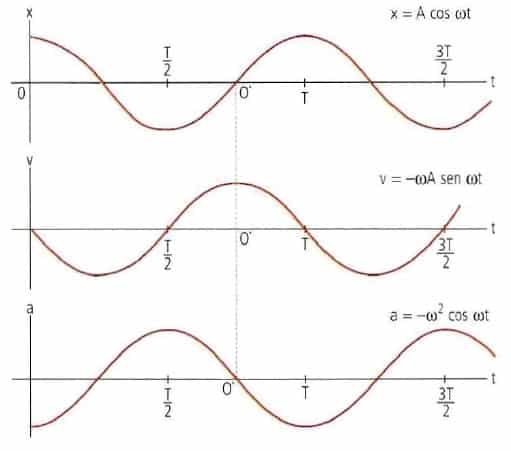
Por ejemplo, en el caso de un sistema masa-resorte, que se saca de su posición de equilibrio hasta una distancia A y se suelta desde el reposo a partir de esta posición, se observa que las soluciones para x(t), v(t) y a(t), cumplen con las condiciones inicia les de que en t = O, Xi = A y Vi= 0.
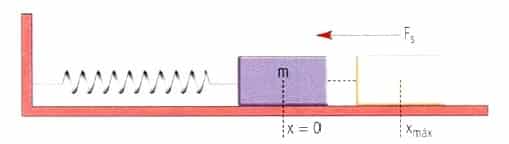
Las siguientes gráficas describen el comportamiento del sistema masa-resorte de acuerdo a las condiciones iniciales para x(t), v(t) y a(t) en su MAS.
